三角形内角和是多少（利用多种方法证明三角形的内角和是180°）

在小学数学中，我们学习了三角形的内角和定理，知道了三角形的内角和为180°。对于这个定理，我们可以利用多种方法进行证明，以下是我从几个不同的方面总结的几种证明方法，现拿来分享，以拓宽学生的思维：

求证：三角形三个内角的和等干180°

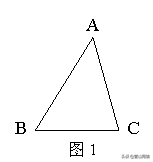
已知：如图1，∠A、∠B、∠C分别为三角形ABC的三个内角，

求证：∠A+∠B+∠C=180°

分析：当我们碰到新问题感觉无法下手时，通常我们可以将新问题通过各种方法转化为已经学过的问题进行证明，这样的方法在初中的几何学中经常会用到，它可以为我们解决新问题带来很大的帮助。证明三角形的内角和，就可以运用这种方法。我们先想想在那些地方碰到过关于180°的角的问题，这会给我们的证明拓宽一定的思路。

思路1：在小学里我们在说明这个问题时是用一张三角形的纸片。将三角形的三个角剪下来，然后拼在一起，从而得到一个平角。说明三角形的内角和为180°。

思路2：然而，不是所有的三角形都可以剪的下来。今天，要证明三角形的三个内角之和等于180°，虽然不能用以前的老方法，但思路和以前有些相似，我们学过一个平角是180°，那么，是否能够设法将三角形的三个内角拼成一个平角，从而，进行说明呢？为此，用辅助线构造出一个平角，再用平行线"移动"内角，将其集中起来。

思路3： 我们知道，当两条平行线被第三条直线所截时的同旁内角互补，也就是它们的和为180°，那么，能否将三角形的三个内角集中到平行线的一组同旁内角上来呢?因此，我们想办法将三角形的三个内角放在两条平行线的两同旁内角的位置上。

利用第一种思路用一张三角形的纸片，将三角形的三个角剪下来，然后拼在一起，从而组成一个平角。但组成的角是不是就是一个标准的平角呢再加上手工时的误差，所以很难清楚的进行说明，跟何况不是所有的三角形都可以剪的下来。因此，在这里，我主要是根据后面的两种思路，总结出下面的几种证明方法。

利用第二种思路得到下列几种证明方法：

证法1 ：如图2，延长边BC到D，并过顶点C作CE∥BA；

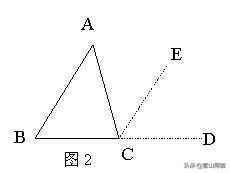
∵CE∥BA（作图）

∴∠1=∠A(两直线平行，内错角相等)，

∠2=∠B(两直线平行，同位角相等).

又∵∠1+∠2+∠ACB＝180° (平角的定义)，

∴∠A+∠B+∠ACB＝180°.

证法： 如图3，过顶点C作DE∥AB；

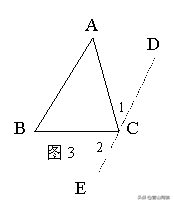
∵DE∥AB（作图）

∴∠1＝∠A，∠2＝∠B(两直线平行，内错角相等)．

又∵∠1+∠ACB+∠2＝180°(平角的定义)，

∴∠A+∠ACB+∠B＝180°

证法3：如图4，在BC边上任取一点D，作DE∥BA，DF∥CA，分别交AC于E，交AB于F；

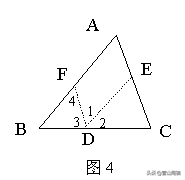
则∠2＝∠B，∠3＝∠C(两直线平行，同位角相等)，

∠1＝∠4(两直线平行，内错角相等)，

∠4＝∠A(两直线平行，同位角相等)，

∴∠1＝∠A(等量代换).

又∵∠1+∠2+∠3＝180°(平角的定义)，

∴∠A+∠B+∠C＝180°.

证法4： 如图5， 作BC的延长线CD，在△ABC的外部以CA为一边，CE为另一边画∠1＝∠A；（也可以直接作CE∥BA）

于是CE∥BA(内错角相等，两直线平行).

∴∠B＝∠2(两直线平行，同位角相等).

又∵∠1+∠2+∠ACB＝180°(平角的定义)，

∴∠A+∠B+∠ACB=180°.

证法5：如图6，在△ABC的内部任取一点D，连结AD、BD，并延长分别交边BC、AC于点E、F，再连结CD；

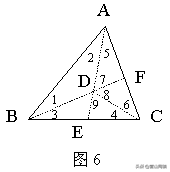
则∠7=∠1+∠2，∠8＝∠3+∠4，∠9=∠5+∠6(三角形的任何一个外角等于和它不相邻的两个内角的和).

又∵∠7+∠8+∠9=180° (平角的定义)，

∴∠1+∠2+∠3+∠4+∠5+∠6=180°.

即∠BAC+∠ABC+∠ACB=180°．

根据第三种思路，也可以设计出几种证法，证法如下：

证法6：如图7，过顶点C作CD∥BA；

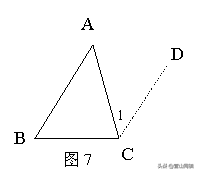
则∠1＝∠A(两直线平行，内错角相等)．

∵CD∥BA.

∴∠1+∠ACB+∠B＝180°(两直线平行，同旁内角互补)．

∴∠A+∠ACB+∠B＝180°.

证法7 ：如图8 ，任意作线段AD交BC于D，分别过点B、C作BE∥DA，CF∥DA；

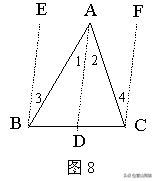
则∠1＝∠3，∠2＝∠4(两直线平行，内错角相等).

∵BE∥DA，CF∥DA，

∴BE∥CF.

∴∠3+∠ABC+∠ACB+∠4＝180°(两直线平行，同旁内角互补)．

∴∠1+∠ABC+∠ACB+∠2＝180°.

∴∠BAC+∠ABC+∠ACB＝180°.

上面用到的几种证明方法，都是将新问题通过各种方法转化为已经学过的问题进行证明，这样的方法在初中的几何学中经常会用到，有些书上将这种思路叫做化归思想。这种思想是一种重要的解题方法，它在我们做题时可以帮助我们确定思考的方向，因此，有必要让学生掌握。